Há algum tempo me deparei com uma code question muito interessante sobre árvores. Não, isso não tem a ver com o problema do desmatamento ou com agricultura. Code questions são desafios de programação que frequentemente envolvem conceitos de Estrutura de Dados, Álgebra, Geometria Analítica, Teoria dos Grafos e uma boa capacidade de analisar e resolver problemas. Pena que muitas vezes isso me falta! :b
Code questions podem parecer algo fora da realidade prática, mas na verdade ajudam muito com o raciocínio e, principalmente, no uso correto de estruturas de dados. Diariamente usamos listas, conjuntos, árvores, pilhas e mapas, muitas vezes de forma equivocada. Por falta de treino, frequentemente temos dificuldades de criar lógicas simples e eficientes.
O problema
A referida questão envolvia o conceito de LCA (Lower Common Ancestor – Ancestral comum mais próximo), derivado da Teoria dos Grafos. LCA é o “pai” (ancestral) mais próximo de dois nós de uma árvore.
Se você não entendeu, pense na hierarquia de uma empresa. Temos o presidente como o topo ou raiz da árvore, os gerentes logo abaixo dele e em seguida subgerentes ou subordinados. Se houver um problema entre dois funcionários quaisquer, precisamos descobrir quem pode responder por ambos. Não podemos ir direto ao presidente, nem “pular” a hierarquia, mas devemos ir ao gerente mais baixo da hierarquia que seja chefe diretamente ou indiretamente de ambos.
Bem, na verdade existe um caso onde o LCA e o exemplo da empresa não são equivalentes. Se os dois nós da árvore que estou procurando forem pai e filho, por exemplo, a resposta para o algoritmo seria o próprio pai. Porém, se numa empresa ocorre um problema entre gerente e subordinado, não deveria ser o gerente o responsável por tratar do assunto. Hum… pensando bem, isso se aplica a muitas empresas, sim.
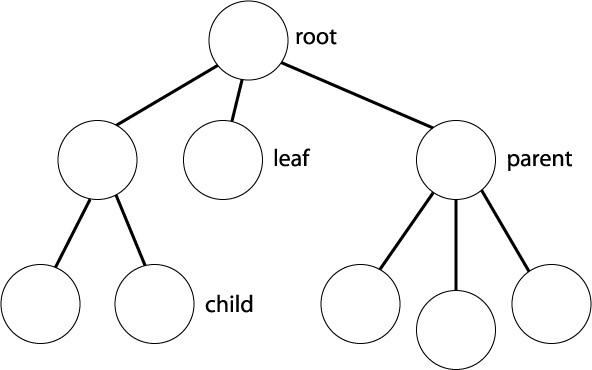
Para entender visualmente uma árvore, considere a imagem abaixo:
Encontrar o ancestral mais comum é simples se cada nó da árvore tiver a informação de quem é seu ancestral. Basta localizar o par de nós e compara os seus pais. Porém, sem essa informação, temos que percorrer a árvore toda armazenando a informação de parentesco antes de fazer essa comparação. Obviamente a code question exigia o caso mais difícil.
Para piorar, a maioria das implementações disponíveis são para Árvores Binárias, isto é, a quantidade de descendentes de cada nó é de no máximo em dois. Isso facilita a solução, mas minha questão era mais complicada, pois cada nó poderia ter vários filhos.
Veja a seguir os atributos de um nó da árvore:
class Node {
Integer id;
List<Node> filhos;
}
Para resolver essa code question, precisamos de um algoritmo para encontrar o LCA, tendo como entrada dois nós com a estrutura do código acima.
Solução recursiva
Primeiramente fiz uma implementação recursiva baseada num algoritmo publicado numa resposta do StackOverflow.
O método ficou assim:
Node findClosestCommonAncestor(Node root, Node p, Node q) {
if (root == null) {
return null;
}
if(root == p || root == q) {
return root;
} else {
Node aux = null;
//if two children contains p and q, root is the ancestor
for (Node current : root.children) {
Node child = findClosestCommonAncestor(current, p, q);
if (child != null) {
if (aux == null) {
aux = child;
} else {
return root;
}
}
}
if (aux != null) return aux;
}
return null;
}
É possível editar e executar esse código no site ideone.
O algoritmo acima basicamente analisa recursivamente cada nó e verifica se dois de seus filhos são o par de nós p e q. Quando um nó puder responder por ambos, temos a resposta.
Solução iterativa
Soluções recursivas são boas, e em alguns casos podem ser as mais eficientes. Porém, é sempre um desafio pensar numa solução iterativa, isto é, usando apenas laços e estruturas como pilhas.
A Wikipedia contém uma página sobre Tree Traversal que inclui pseudo-códigos para iterar sobre árvore binárias usando pilhas. Existem várias formas de iterar sobre uma árvore. Por exemplo, o código abaixo é do Pre-order Traversal, que significa percorrer os nós começando do nó mais à esquerda até acabar no mais da direita:
iterativePreorder(node)
parentStack = empty stack
while (not parentStack.isEmpty() or node ≠ null)
if (node ≠ null)
visit(node) #1
parentStack.push(node) #2
node = node.left
else
node = parentStack.pop() #3
node = node.right
Anotei três pontos (#1, #2, #3), os quais irei comentar mais adiante.
Entretanto, para a resolução do nosso problema não estamos limitados a dois descendentes por nó, então são necessários alguns ajustes:
- Uma pilha auxiliar para armazenar o filho atual sendo visitado a cada nível que o algoritmo desce na árvore. Diferente de uma árvore binária, onde basta percorrer o nó da esquerda e depois o da direita, para percorrer um nó com
nfilhos precisamos de um contador. E como cada filho pode termfilhos, então deve haver um contador para cada nível da árvore. - Uma segunda pilha auxiliar para armazenar o caminho até o primeiro nó encontrado. Como um dos objetivos do algoritmo é encontrar dois nós, devemos armazenar o caminho até o primeiro e continuar até encontrar o segundo.
Um pseudo-código para encontrar o ancestral mais próximo dos nós p e q, dada a raiz node, ficou assim:
findClosestCommonAncestor(node, p, q)
parentStack = empty stack
childIndexStack = empty stack
firstNodePath = null
while (not parentStack.isEmpty() or node ≠ null)
if (node ≠ null)
#1
if (node == p || node == q)
if (firstNodePath ≠ null)
parentStack.add(node)
int n = min(parentStack.length, firstNodePath.length)
for i = (n - 1)..0
if (parentStack(i) == firstNodePath(i))
return parentStack(i)
return null
else
firstNodePath = copy parentStack
firstNodePath.push(node)
#2
if (not empty node.children)
parentStack.push(node)
childIndexStack.push(0)
node = node.children(0)
else
node = null
else
#3
node = parentStack.peek()
i = childIndexStack.pop() + 1
if (i >= node.children.length)
node = null
parentStack.pop()
else
node = node.children(i)
childIndexStack.push(i)
Certamente ficou mais complexo, mas o conceito é basicamente o mesmo do anterior. Note que também marquei neste algoritmo três pontos, pois são análogos ao anterior. Vejamos:
- #1 Este é o bloco onde o valor do nó atual é processado. O
visit(node)do primeiro algoritmo foi substituído por um bloco que verifica se um dos nós foi encontrado. Caso tenha encontrado o primeiro nó ele salva a pilha atual. Caso tenha encontrado os dois ele compara as pilhas, item a item, procurando pelo pai mais próximo. - #2 O algoritmo inicial adiciona o nó atual na pilha e avança para o filho da esquerda. O segundo algoritmo generaliza para
nfilhos avançando para o primeiro filho (0). - #3 O algoritmo inicial desempilha um nó e avança para o filho da direita. O segundo algoritmo generaliza avançando para o próximo filho (anterior + 1).
O código em Java ficou assim:
class Node {
List<Node> children = new ArrayList<Node>();
Integer id;
Node(Integer id) {
this.id = id;
}
}
Node findClosestCommonAncestor(Node node, Node p, Node q) {
Stack<Node> parentStack = new Stack<Node>();
Stack<Integer> childIndexStack = new Stack<Integer>();
Stack<Node> firstNodePath = null;
while (!parentStack.empty() || node != null) {
if (node != null) {
if (node == p || node == q) {
if (firstNodePath != null) {
parentStack.add(node);
int n = Math.min(parentStack.size(), firstNodePath.size());
for (int i = n - 1; i >= 0; i--) {
if (parentStack.get(i) == firstNodePath.get(i)) {
return parentStack.get(i);
}
}
return null;
} else {
firstNodePath = new Stack<Node>();
firstNodePath.setSize(parentStack.size());
Collections.copy(firstNodePath, parentStack);
firstNodePath.push(node);
}
}
if (!node.children.isEmpty()) {
parentStack.push(node);
childIndexStack.push(0);
node = node.children.get(0);
} else {
node = null;
}
} else {
node = parentStack.peek();
Integer i = childIndexStack.pop() + 1;
if (i >= node.children.size()) {
node = null;
parentStack.pop();
} else {
node = node.children.get(i);
childIndexStack.push(i);
}
}
}
return null;
}
A versão completa do código Java está disponível para edição e teste no ideone.com.
Considerações
Se você é um leitor ocasional, não se preocupe se não entendeu nada dos códigos acima. Isso não é algo que você pega em cinco minutos. Por exemplo, eu passei alguns dias pensando na solução iterativa. É necessário estar “imerso” no problema.
Este artigo pode parecer dissonante em relação ao conteúdo do site, mas aprendi recentemente que estudar algoritmos deve fazer parte do aperfeiçoamento de todo desenvolvedor sério. Para usar tecnologias de ponta e de alto nível isso é essencial. Na verdade, não conhecer a teoria da computação é o principal motivo pelo qual temos dificuldades em entender e aplicar melhores soluções.
Você acha que empresas como Google, Facebook ou Amazon conseguem atender milhões de usuários simultânea e ininterruptamente usando implementações padrão de mercado? Os profissionais que mantêm grandes estruturas funcionando são os que entendem profundamente os fundamentos da computação, não APIs básicas de linguagens de programação.
Por muito tempo eu mesmo menosprezei esse tipo de conhecimento, considerando que não agregaria muito à minha carreira. Eu queria algo de “alto nível” e a teoria parecia perda de tempo. Estava errado!
O mercado de trabalho brasileiro ajuda a criar essa ilusão. Veja as vagas publicadas por aí. Eles pedem lógica, Inglês e uma lista infindável de frameworks. Então você sai freneticamente aprendendo várias coisas que, na verdade, são mais do mesmo.
Então um dia você acorda e percebe que é mais um programador medíocre que só sabe uma lista de frameworks. E pior, descobre que na prática as empresas nem mesmo valorizam esse conhecimento.
Este artigo foi baseado numa questão do StackOverflow em Português!